 Gradient Controller
Gradient Controller
Gradient Controller
A gradient controller is a composite of a gradient limiter and a following feedback controller. The gradient limiter limits one or two derivatives of the setpoint. This may be used for a comfort increase of a speed controller or to reduce the wear of a power drive. Here the feedback controller for the process G is a PI controller with feed forward of the setpoint.
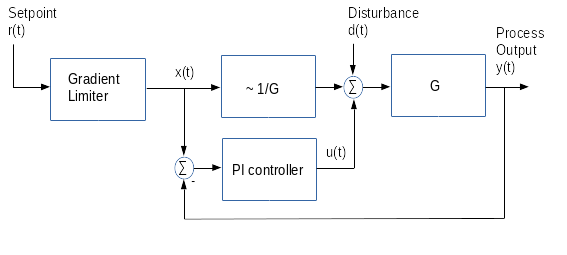
Gradient Limiter for one Derivative
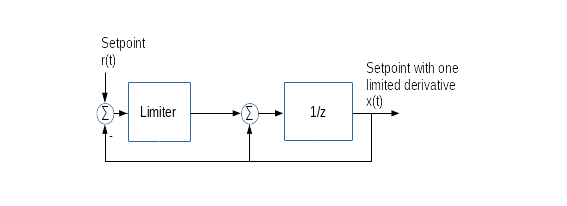
Gradient Limiter for two Derivatives
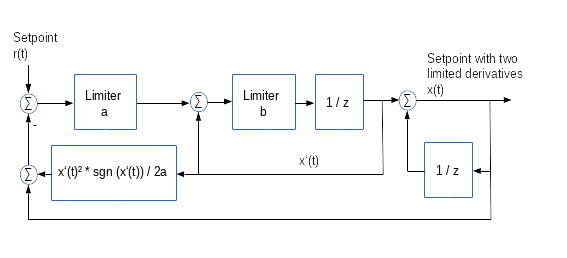
Step Response of a Gradient Limiter for two Derivatives
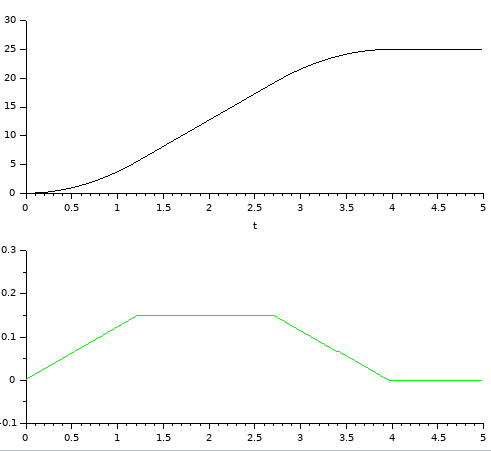
On top x(t) and below x'(t)